1.7. Основные формулы комбинаторики

При нахождении вероятностей в схеме классического определения широко используется комбинаторика, поэтому напомним наиболее употребительные определения и формулы для вычисления.

Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества.

Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок

Р n = n !

Заметим, что удобно рассматривать 0!, полагая, по определению, 0! = 1.

Пример . Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз?

Решение . Искомое число трехзначных чисел Р 3 = 3! = 123 = 6.

Размещениями n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений

Пример . Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?

Решение . Искомое число сигналов
.

Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний

.

Пример . Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?

Решение . Искомое число способов
.

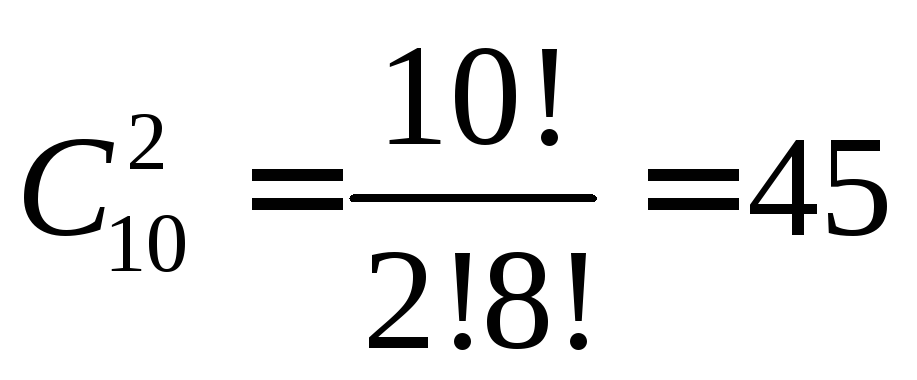Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством

Замечание . Выше предполагалось, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам. Например, если среди n элементов есть n 1 элементов одного вида, n 2 элементов другого вида и т. д., то число перестановок с повторениями

,

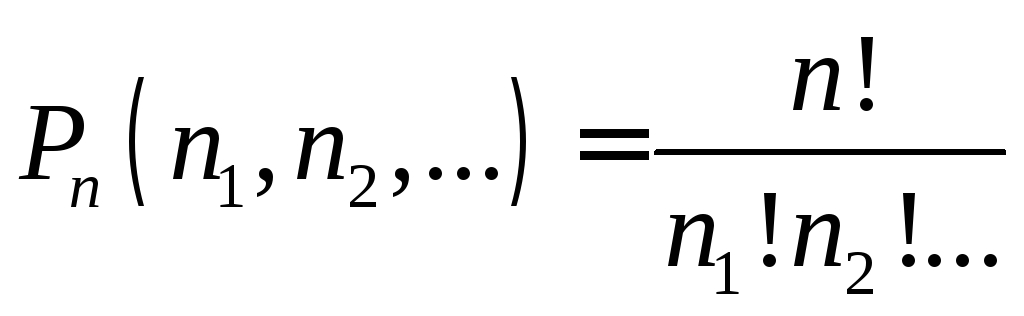где n 1 + n 2 + ... = n .

При решении задач комбинаторики используют следующие правила:

1. Правило суммы. Если некоторый объект A может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А , либо В можно m + n способами.

2. Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А , В ) в указанном порядке может быть выбрана mn способами.

Приведем несколько примеров непосредственного вычисления вероятностей.

Пример 1. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.

Решение. Обозначим через А событие – набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных элементарных исходов равно 10. Эти исходы несовместны, равновозможны и образуют полную группу. Благоприятствует событию А лишь один исход (нужная цифра лишь одна). Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

Р (А )=1/10.

Пример 2. Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.

Решение. Обозначим через В событие – набраны две нужные цифры. Всего можно набрать столько различных цифр, сколько может быть составлено размещений из десяти цифр по две, т.е.
. Таким образом, общее число возможных элементарных исходов равно 90. Эти исходы несовместны, равновозможны и образуют полную группу. Благоприятствует событию В лишь один исход. Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

Р (В )=1/90.

Пример 3. Указать ошибку «решения» задачи: «Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 4 (событие А )».

Решение. Всего возможны 2 исхода испытания: сумма выпавших очков равна 4, сумма выпавших очков не равна 4. Событию А благоприятствует один исход; общее число исходов равно двум. Следовательно, искомая вероятность

Р (А ) = 1/2.

Ошибка этого решения состоит в том, что рассматриваемые исходы не являются равновозможными.

Правильное решение . Общее число равновозможных исходов испытания равно 66 = 36 (каждое число выпавших очков на одной кости может сочетаться со всеми числами очков другой кости). Среди этих исходов благоприятствуют событию А только 3 исхода: (1; 3), (3; 1), (2; 2) (в скобках указаны числа выпавших очков). Следовательно, искомая вероятность

Р (А ) = 3/36 = 1/12.

Пример 4. В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди шести взятых наудачу деталей 4 стандартных.

Решение. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10, т. е. числу сочетаний из 10 элементов но 6 элементов ().

Определим число исходов, благоприятствующих интересующему нас событию А (среди шести взятых деталей 4 стандартных). Четыре стандартные детали можно взять на семи стандартных деталей способами; при этом остальные 6 – 4 = 2 детали должны быть нестандартными; взять же 2 нестандартные детали из 10 – 7 = 3 нестандартных деталей можноспособами. Следовательно, число благоприятствующих исходов равно
.

Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

При решении многих практических задач приходится использовать комбинации элементов, выбирать из данной совокупности те, которые имеют определенные свойства, и размещать их в определенном порядке. Такие задачи называются комбинаторными . Раздел математики, посвящённый решению задач выбора и расположения элементов в соответствии с данными условиями, называется комбинаторикой. Термин «комбинаторика» происходит от латинского слова «combina» , что в переводе на русский язык означает – «сочетать», «соединять».

Выбранные группы элементов называют соединениями. Если все элементы соединения разные, то получаем соединения без повторений, которые и рассмотрим ниже.

Большинство комбинаторных задач решается с помощью двух основных правил – правила суммы и правила произведения .

Задача 1.

В магазине «Все для чая» есть 6 разных чашек и 4 разных блюдца. Сколько вариантов чашки и блюдца можно купить?

Решение .

Чашку мы можем выбрать 6-ю способами, а блюдце 4-я способами. Так как нам надо купить пару чашку и блюдце, то это можно сделать 6 · 4 = 24 способами (по правилу произведения).

Ответ: 24.

Для успешного решения комбинаторных задач надо еще и правильно выбрать формулу, по которой искать количество нужных соединений. В этом поможет следующая схема.

Рассмотрим решение нескольких задач на разные виды соединений без повторений.

Задача 2.

Найдите количество трехзначных чисел, которые можно составить из цифр 1, 2, 3, 4, 5, 6, 7, если цифры в числе повторяться не могут.

Решение.

Для выбора формулы выясняем, что для чисел, которые мы будем составлять, порядок учитывается и не все элементы одновременно выбираются. Значит, это соединение – размещение из 7 элементов по 3. Воспользуемся формулой для числа размещений: A 7 3 = 7(7 – 1)(7 – 2) = 7 · 6 · 5 = 210 чисел.

Ответ: 210.

Задача 3.

Сколько существует семизначных телефонных номеров, в которых все цифры разные, а номер не может начинаться с нуля?

Решение.

На первый взгляд эта задача такая же, как и предыдущая, но сложность в том, что надо не учитывать те соединения, которые начинаются с нуля. Значит необходимо из существующих 10-ти цифр составить все семизначные номера телефонов, а потом от полученного числа отнять количество номеров, начинающихся с нуля. Формула будет иметь вид:

A 10 7 – A 9 6 = 10 · 9 · 8 · 7 · 6 · 5 · 4 – 9 · 8 · 7 · 6 · 5 · 4 = 544 320.

Ответ: 544 320.

Задача 4.

Сколькими способами можно расставить на полке 12 книг, из которых 5 книг – это сборники стихотворений, так, чтобы сборники стояли рядом?

Решение.

Сначала примем 5 сборников условно за одну книгу, потому что они должны стоять рядом. Так как в соединении существенным есть порядок, и все элементы используются, значит это перестановки из 8 элементов (7 книг + условная 1 книга). Их количество Р 8 . Далее будем переставлять между собой только сборники стихотворений. Это можно сделать Р 5 способами. Поскольку нам нужно расставить и сборники, и другие книги, то воспользуемся правилом произведения. Следовательно, Р 8 · Р 5 = 8! · 5!. Число способов будет большим, поэтому ответ можно оставить в виде произведения факториалов.

Ответ: 8! · 5!

Задача 5 .

В классе 16 мальчиков и 12 девочек. Для уборки территории возле школы нужно 4 мальчика и 3 девочки. Сколькими способами можно их выбрать со всех учеников класса?

Решение.

Сначала отдельно выберем 4 мальчика из 16 и 3 девочки из 12. Так как порядок размещения не учитывается, то соответственные соединения – сочетания без повторений. Учитывая необходимость одновременного выбора и мальчиков, и девочек, используем правило произведения. В результате число способов будет вычисляться таким образом:

С 16 4 · С 12 3 = (16!/(4! · 12!)) · (12!/(3! · 9!)) = ((13 · 14 · 15 · 16) / (2 · 3 · 4)) ·((10 · 11 · 12) / (2 · 3)) = 400 400.

Ответ: 400 400.

Таким образом, успешное решение комбинаторной задачи зависит от правильного анализа ее условия, определения типа соединений, которые будут составляться, и выбора подходящей формулы для вычисления их количества.

Остались вопросы? Не знаете, как решать комбинаторные задачи?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

КОМБИНАТОРИКА

Комбинаторика - раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.

Правила сложения и умножения в комбинаторике

Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В - n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.

Пример 1.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?

Решение

Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.

По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.

Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n 1 способами, второе действие n 2 способами, третье - n 3 способами и так до k-го действия, которое можно выполнить n k способами, то все k действий вместе могут быть выполнены:

способами.

Пример 2.

В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?

Решение

Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.

После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.

По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.

Сочетания без повторений. Сочетания с повторениями

Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?

Пример 3.

Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?

Решение

Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

.

Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?

.

Пример 4.

В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Решение

Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

.

Размещения без повторений. Размещения с повторениями

Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?

Пример 5.

В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?

Решение.

В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:

Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.

Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно вы б рать и разместить по m различным местам m из n предметов, с реди которых есть одинаковые?

Пример 6.

У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера- составить каталог. Сколько различных пятизначных номеров может составить мальчик?

Перестановки без повторений . Перестановки с повторениями

Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?

Пример 7.

Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?

Решение

Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.

Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k < n), т. е. есть одинаковые предметы.

Пример 8.

Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?

Решение

Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно

ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ "КОМБИНАТОРИКА"

Лекция 2

Согласно классическому определению подсчет вероятности события А сводится к подсчету числа благоприятствующих ему исходов. Делают это обычно комбинаторными методами.

Комбинаторика раздел математики, в котором изучаются задачи выбора элементов из заданного множества и расположения их в группы по заданным правилам, в частности задачи о подсчете числа комбинаций (выборок), получаемых из элементов заданного конечного множества. В каждой из них требуется подсчитать число возможных вариантов осуществления некоторого действия, ответить на вопрос «сколькими способами?».

Многие комбинаторные задачи могут быть решены с помощью следующих двух важных правил, называемых соответственно правилами умножения и сложения.

Правило умножения (основной принцип): если из некоторого конечного множества первый объект (элемент x) можно выбрать n способами и после каждого такого выбора второй объект (элемент у) можно выбрать m способами, то оба объекта (x и y) в указанном порядке можно выбрать n´m способами.

Этот принцип, очевидно, распространяется на случай трех и более объектов.

Пример 1. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если:

а) цифры не повторяются?

б) цифры могут повторяться?

Имеется 5 различных способов выбора цифры для первого места (слева в трехзначном числе). После того как первое место занято, например, цифрой 2, осталось четыре цифры для заполнения второго места. Для заполнения третьего места остается выбор из трех цифр. Следовательно, согласно правилу умножения имеется 5×4×3 = 60 способов расстановки цифр, т. е. искомое число трехзначных чисел есть 60. (Вот некоторые из этих чисел: 243, 541, 514, 132, ...) Понятно, что если цифры могут повторяться, то трехзначных чисел 5×5×5= 125. (Вот некоторые из них: 255, 333, 414, 111, 122, ...)

Правило суммы. Если некоторый объект х можно выбрать n способами, а объект у можно выбрать m способами, причем первые и вторые способы не пересекаются, то любой из указанных объектов (х или у), можно выбрать n+m способами.

Это правило распространяется на любое конечное число объектов.

Пример 2. В студенческой группе 14 девушек и 6 юношей. Сколькими способами можно выбрать, для выполнения различных заданий, двух студентов одного пола?

По правилу умножения двух девушек можно выбрать 14×13 = 182 способами, а двух юношей - 6×5 = 30 способами. Следует выбрать двух студентов одного пола: двух студенток или двух юношей. Согласно правилу сложения таких способов выбора будет 182 + 30 = 212.

Решение вероятностных (и не только их) задач часто облегчается, если использовать комбинаторные формулы. Каждая из них определяет число всевозможных исходов в некотором опыте (эксперименте), состоящем в выборе наудачу m элементов из n различных элементов рассматриваемого множества.

Существуют две схемы выбора m элементов (0 < m £ n) из исходного множества: без возвращения (без повторений) и с возвращением (с повторением). В первом случае выбранные элементы не возвращаются обратно; можно отобрать сразу все m элементов или последовательно отбирать их по одному. Во второй схеме выбор осуществляется поэлементно с обязательным возвращением отобранного элемента на каждом шаге.

Схема выбора без возвращений

Пусть дано множество, состоящее из n различных элементов.

Размещением из n элементов по m элементов (0 < m £ n) называется любое упорядоченное подмножество данного множества, содержащее m элементов.

Из определения вытекает, что размещения - это выборки (комбинации), состоящие из m элементов, которые отличаются друг от друга либо составом элементов, либо порядком их расположения.

Число размещений из n элементов по m элементов обозначается символом («А из эн по эм») и вычисляется по формуле

Для составления размещения надо выбрать m элементов из множества с n элементами и упорядочить их, т. е. заполнить m мест элементами множества. Первый элемент можно выбрать n способами, т. е. на первое место можно поместить любой из n элементов. После этого второй элемент можно выбрать из оставшихся n-1 элементов n-1 способами. Для выбора третьего элемента имеется n-2 способа, четвертого - n-3 способа, и, наконец, для последнего m-го элемента - (n-(m-1)) способов. Таким образом, по правилу умножения, существует n(n-1)(n-2)...(n-(m-1)) способов выбора m элементов из данных n элементов, т. е. .

Пример 3. Составить различные размещения по 2 из элементов множества D = {а, b, с}; подсчитать их число.

Из трех элементов можно образовать следующие размещения по два элемента: (а, b), (b, а), (а, с), (с, а), (b, с), (с, b). Согласно формуле (1) их число: = 3×2 = 6.

Перестановкой из n элементов называется размещение из n элементов по n элементов.

Из определения вытекает, что перестановки - это выборки (комбинации), состоящие из n элементов и отличающиеся друг от друга только порядком следования элементов. Число перестановок из n элементов обозначается символом Р n («пэ из эн») и вычисляется по формуле

Формула (3) следует из определения перестановки:

Пример 4. Составить различные перестановки из элементов множества Е={2, 7, 8}; подсчитать их число.

Из элементов данного множества можно составить следующие перестановки: (2,7,8); (2,8,7); (7,2,8); (7,8,2); (8,2,7); (8,7,2). По формуле (3) имеем: Р 3 = 3! = 1×2×3 = 6.

Пример 5. Сколькими способами можно расставить на полке 5 различных книг?

Искомое число способов равно числу перестановок из 5 элементов (книг), т. е.

Р 5 =5!=1×2×3×4×5 = 120.

Сочетанием из n элементов по m (0 < m £ n) элементов называется любое подмножество, которое содержит m элементов данного множества.

Из определения вытекает, что сочетания - это выборки (комбинации), каждая из которых состоит из m элементов, взятых из данных n элементов, и которые отличаются друг от друга хотя бы одним элементом, т. е. отличаются только составом элементов.

Число сочетаний из n элементов по m элементов обозначается символом («цэ из эн по эм») и вычисляется по формуле

Число размещений из n элементов по m элементов можно найти следующим образом: выбрать m элементов из множества, содержащего n элементов (это можно сделать способами); затем в каждом из полученных сочетаний (подмножеств) сделать все перестановки для упорядочения подмножеств (это можно сделать Р m способами). Следовательно, согласно правилу умножения, можно записать:

Отсюда или

Можно показать, что имеют место формулы:

Пример 5. Составить различные сочетания по 2 из элементов множества D - {а, b, с}; подсчитать их число.

Из трех элементов можно образовать следующие сочетания по два элемента: (а, b); (a,с); (b,с). Их число: (формула (4)).

Пример 6. Сколькими способами можно выбрать 3 цветка из вазы, в которой стоят 10 красных и 4 розовых гвоздики? А если выбрать 1 красную гвоздику и 2 розовых?

Так как порядок выбора цветов не имеет значения, то выбрать 3 цветка из вазы, в которой стоят 14 гвоздик, можно способами. По формуле (4) находим: . Далее: красную гвоздику можно выбрать способами. Выбрать две розовые гвоздики из имеющихся четырех можно способами. Поэтому букет из одной красной и двух розовых гвоздик можно составить, по правилу умножения, способами.

Схема выбора с возвращением

Если при выборке m элементов из n элементы возвращаются обратно и упорядочиваются, то говорят, что это размещения с повторениями .

Размещения с повторениями могут отличаться друг от друга элементами, их порядком и количеством повторений элементов. Число всех размещений из n элементов по m с повторениями обозначается символом и вычисляется по формуле (6)

Пример 7. Из 3 элементов а, b, с составить все размещения по два элемента с повторениями.

По формуле (1.12) число размещений по два с повторениями равно . Это: (а,а), (а,b), (а, с), (b,b), (b,а), (b,с), (с,с), (с,а), (с, b)

Пример 8. Сколько пятизначных чисел можно составить, используя цифры:

а) Все пятизначные числа, составленные из цифр 2. 5, 7, 8, отличаются друг от друга либо порядком их следования (например, 25558 и 52855), либо самими цифрами (например, 52788 и 78888). Следовательно, они являются размещениями из 4 элементов по 5 с повторениями, т.е. . Таким образом, искомое число пятизначных чисел равно . Этот же результат можно получить, используя правило умножения: первую цифру слева в пятизначном числе можно выбрать четырьмя способами, вторую - тоже четырьмя способами, третью - четырьмя, четвертую - четырьмя, пятую - четырьмя. Всего получается 4×4×4×4×4=1024 пятизначных чисел.

б) Если пятизначные числа состоят из цифр 0, 1, 9, то первую цифру слева можно выбрать двумя способами (0 не может занимать первую позицию), каждую из оставшихся четырех цифр можно выбрать тремя способами. Согласно правилу умножения, таких чисел будет 2×3×3×3×3=162. (Иначе: .)

Если при выборке m элементов из n элементы возвращаются обратно без последующего упорядочивания, то говорят, что это сочетания с повторениями .

Число всех сочетаний из n элементов по m с повторениями обозначается символом и вычисляется по формуле

Пример 9. Из трех элементов а, b, с составить все сочетания по два элемента с повторениями.

По формуле (7) число сочетаний по два с повторениями равно . Составляем эти сочетания с повторениями: (а, а), (a. b), (а, с), (b,b), (b, с), (с, с).

Пример 10. Сколькими способами можно составить букет из 5 цветов, если в наличии есть цветы трех сортов?

Рассматриваемое множество состоит из трех различных элементов, а выборки имеют объем, равный 5. Поскольку порядок расположения цветов в букете не играет роли, то искомое число букетов равно числу сочетаний с повторениями из трех элементов по 5 в каждом. По формуле (7) имеем

Пусть в множестве с n элементами есть k различных элементов, при этом 1-й элемент повторяется n 1 раз, 2-й элемент - n 2 раз..., к-й элемент - n k раз, причем n 1 +n 2 +…+n k =n.

Перестановки из n элементов данного множества называют перестановками с повторениями из n элементов.

Число перестановок с повторениями из n элементов обозначается символом

Р n (n 1 , n 2 , … ,n k) и вычисляется по формуле

Пример 11. Сколько различных пятизначных чисел можно составить из цифр 3, 3, 5, 5, 8?

Применим формулу (8). Здесь n=5, n 1 =2, n 2 =2, n 3 = 1. Число различных пятизначных чисел, содержащих цифры 3, 5 и 8, равно

Комбинаторикой называется раздел математики, изучающий вопрос о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).

Правило умножения (основная формула комбинаторики)

Общее число способов, которыми можно выбрать по одному элементу из каждой группы и расставить их в определенном порядке (то есть получить упорядоченную совокупность ), равно:

Пример 1

Монету подбросили 3 раза. Сколько различных результатов бросаний можно ожидать?

Решение

Первая монета имеет альтернативы – либо орел, либо решка. Для второй монеты также есть альтернативы и т.д., т.е. .

Искомое количество способов:

Правило сложения

Если любые две группы и не имеют общих элементов, то выбор одного элемента или из , или из , …или из можно осуществить способами.

Пример 2

На полке 30 книг, из них 20 математических, 6 технических и 4 экономических. Сколько существует способов выбора одной математической или одной экономической книги.

Решение

Математическая книга может быть выбрана способами, экономическая - способами.

По правилу суммы существует способа выбора математической или экономической книги.

Размещения и перестановки

Размещения – это упорядоченные совокупности элементов, отличающиеся друг от друга либо составом, либо порядком элементов.

Размещения без повторений , когда отобранный элемент перед отбором следующего не возвращается в генеральную совокупность. Такой выбор называется последовательным выбором без возвращения, а его результат – размещением без повторений из элементов по .

Число различных способов, которыми можно произвести последовательный выбор без возвращения элементов из генеральной совокупности объема , равно:

Пример 3

Расписание дня состоит из 5 различных уроков. Определите число вариантов расписания при выборе из 11 дисциплин.

Решение

Каждый вариант расписания представляет набор 5 дисциплин из 11, отличающихся от других вариантов как составом, так и порядком следования. поэтому:

Перестановки – это упорядоченные совокупности, отличающиеся друг от друга только порядком элементов. Число всех перестановок множества из элементов равно

Пример 4

Сколькими способами можно рассадить 4 человек за одним столом?

Решение

Каждый вариант рассадки отличается только порядком участников, то есть является перестановкой из 4 элементов:

Размещения с повторениями , когда отобранный элемент перед отбором следующего возвращается в генеральную совокупность. Такой выбор называется последовательным выбором с возвращением, а его результат - размещением с повторениями из элементов по .

Общее число различных способов, которыми можно произвести выбор с возвращением элементов из генеральной совокупности объема , равно

Пример 5

Лифт останавливается на 7 этажах. Сколькими способами могут выйти на этих этажах 6 пассажиров, находящихся в кабине лифта?

Решение

Каждый из способов распределения пассажиров по этажам представляет собой комбинацию 6 пассажиров по 7 этажам, отличающуюся от других комбинаций как составом, так и их порядком. Так как одном этаже может выйти как один, так и несколько пассажиров, то одни и те же пассажиры могут повторяться. Поэтому число таких комбинаций равно числу размещений с повторениями из 7 элементов по 6:

Сочетания

Сочетаниями из n элементов по k называются неупорядоченные совокупности, отличающиеся друг от друга хотя бы одним элементом.

Пусть из генеральной совокупности берется сразу несколько элементов (либо элементы берут последовательно, но порядок их появления не учитывается). В результате такого одновременного неупорядоченного выбора элементов из генеральной совокупности объема получаются комбинации, которые называются сочетаниями без повторений из элементов по .

Число сочетаний из элементов по равно:

Пример 6

В ящике 9 яблок. Сколькими способами можно выбрать 3 яблока из ящика?

Решение

Каждый вариант выбора состоит из 3 яблок и отличается от других только составом, то есть представляет собой сочетания без повторений из 9 элементов:

Количество способов, которыми можно выбрать 3 яблока из 9:

Пусть из генеральной совокупности объема выбирается элементов, один за другим, причем каждый отобранный элемент перед отбором следующего возвращается в генеральную совокупность. При этом ведется запись, какие элементы появились и сколько раз, однако порядок их появления не учитывается. Получившиеся совокупности называются сочетаниями с повторениями из элементов по .

Число сочетаний с повторениями из элементов по :

Пример 7

На почте продают открытки 3 видов. Сколькими способами можно купить 6 открыток?

Это задача на отыскание числа сочетаний с повторениями из 3 по 6:

Разбиение множества на группы

Пусть множество из различных элементов разбивается на групп так, то в первую группу попадают элементов, во вторую - элементов, в -ю группу - элементов, причем . Такую ситуацию называют разбиением множества на группы.

Число разбиений на групп, когда в первую попадают элементов, во вторую - элементов, в k-ю группу - элементов, равно:

Пример 8

Группу из 16 человек требуется разбить на три подгруппы, в первой из которых должно быть 5 человек, во второй – 7 человек, в третьей – 4 человека. Сколькими способами это можно сделать?